What is Vedic Maths and its Importance?
Vedic Mathematics is an ancient mathematical technique that originated in India. These methods were very helpful to simplify complex mathematical calculations, making them easier and more efficient to solve. Now-a-days this ancient method is gaining more interest due to its effectiveness in simplifying various mathematical operations. In this article we will be discussing the importance of vedic maths.
Benefits of Vedic Maths
- Speed and Efficiency: Vedic Maths provides shortcuts and strategies that enhance the speed and efficiency of calculations, making it a valuable tool in competitive exams.
- Mental Math: Vedic Maths draw attention to mental calculations, reducing dependency on paper and calculators. This not only sharpens your mental ability skills but also boosts confidence in solving mathematical problems.
- Flexibility: The techniques in Vedic Mathematics are flexible and can be applied to a wide range of mathematical problems, from basic arithmetic to more complex calculations.
- Conceptual Understanding: While Vedic Maths offers quick solutions, it also encourages a deeper understanding of mathematical concepts by using principles behind the techniques.
- Cultural Heritage: Learning Vedic Maths allows individuals to connect with the mathematical heritage of ancient India, providing a deep insight into the intellectual advancements of ancient India.
Tricks of Vedic Maths
Vedic Mathematics has many tricks which simplify the calculations across various mathematical operations. Let’s explore some of the vedic math tricks.
Addition Tricks
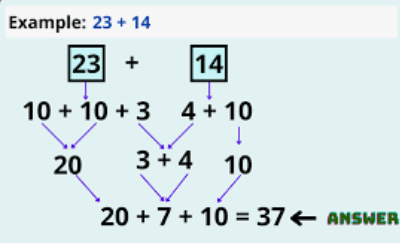
Addition Tricks in vedic math involve splitting numbers and adding the components separately, followed by adjustments. For instance, to add 58 and 46:
Step 1: Split the numbers into tens and units: 50 + 8 and 60 + 6.
Step 2: Add the components: 50 + 40 = 90 and 8 + 6 = 14.
Step 3: Adjust for carry: Since 14 is greater than 10, add 10 to the sum of 90, resulting in 100 + 4 (adjusted value).
Step 4: The final sum is 104.
Example :
- 32 + 57, => (30 + 2) + (50 + 7) => (30 + 50) + (2 + 7) => 80 + 9 = 89.
- 48 + 63, => (40 + 8) + (60 + 3) => (40 + 60) + (8 + 3)=> 100 + 11 = 111.
Subtraction Tricks
Vedic Subtraction Tricks involve similar splitting and adjusting techniques. For instance, to subtract 376 from 589:
Step 1: Split the numbers into components: 500 – 300, 80 – 70, and 9 – 6.
Step 2: Subtract each component: 500 – 300 = 200, 80 – 70 = 10, and 9 – 6 = 3.
Step 3: Combine the results: 200 + 10 + 3 = 213.
Example :
- 48 – 32 => (40 – 30) + (8 – 2 ) => 10 + 6 => 16.
- 489 – 267 => (400 – 200) + (80 – 60) + (9 – 7) => 222.

Squaring Tricks
Vedic Squaring Tricks simplify squaring numbers. For example, to square 35:
Step 1.Choose a base which is closer to the original number.
Step 2. Find the difference of the number from the base.
Step 3. Add the difference with the original number.
Step 4. Multiply the result with the base.
Step 5. Now, add result with the square of the difference
Example :
- (99^2) = ?
Step 1. Choose 100 as base
Step 2. Difference: 99-100 = -1
Step 3. Add the number with the difference that you got = 99 + (-1) = 98
Step 4. Multiplying result with base = 98*100 = 9800
Step 5. Now, add result with the square of the difference= 9800 + (-1)^2 = 9801
So our answer is: (99) ^2 = 9801
2. (49^2) = ?
Step 1. Choose 50 as base
Step 2. Difference: 49-50 = -1
Step 3. Add the number with the difference that you got = 49 + (-1) = 48
Step 4. Multiplying result with base = 48*50 = 2400
Step 5. Now, add result with the square of the difference= 2400 + (-1)^2 = 2401
So our answer is: (49) ^2 = 2401.
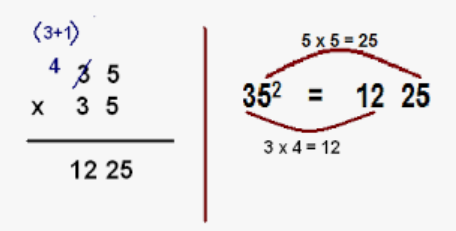
Square Root Tricks
Vedic Square Root Tricks simplify finding square roots. For example, to find the square root of 1764:
Step 1: Split the number into pairs: 17 and 64.
Step 2: Find the largest digit whose square is less than 17 (which is 4), and the remaining digits become the dividend (17 – 16).
Step 3: Approximate the root: The approximate square root is the digit we found in the previous step, which is 4.
Step 4: Adjust the dividend: Subtract the square of the approximate root from the dividend: 1 – 4^2 = 1 – 16 = -15.
Step 5: Divide the adjusted dividend by twice the approximate root: -15 / (2 * 4) = -15 / 8 = -1.875
Step 6: Combine the approximate root (4) and the quotient from the previous step 4 – 1.875 = 2.125.
So, the square root of 1764 is approximately 42.125.
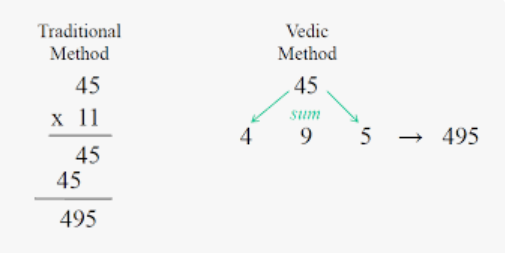
Multiplication Tricks
Vedic Multiplication Tricks offer shortcuts for multiplying numbers (11 – 19).
Step 1: Add the unit digit of the smaller number to the larger number.
Step 2: Multiply the result by 10.
Step 3: Multiply the unit digits of the numbers.
Step 4: Add the two numbers.
Example:
- Multiplying 13 and 15, the answer is 195:
Step 1: 15 + 3 = 18.
Step 2: 18 * 10 = 180.
Step 3: 3 * 5 = 15.
Step 4: Add 180 + 15 = 195.
2. Multiplying 14 and 18, the answer is 336:
Step 1: 18 + 4 = 22.
Step 2: 22 * 10 = 220.
Step 3: 8 * 4 = 32.
Step 4: Add 220 + 32 = 252.
Conclusion of Vedic Maths and Its Importance
Learning Vedic Maths techniques into your mathematical toolkit can revolutionize the way you approach calculations. These methods not only help in solving problems but also promote a deeper understanding of mathematical concepts.
Download PPT of Vedic Maths and its Importance

Video On Vedic Maths and its Importance
FAQs – Vedic Maths and its Importance
Q: What is the trick 5 in Vedic maths?
Ans: Trick 5 in Vedic Maths refers to a specific technique or method used for calculations. Vedic Mathematics consists of various tricks and shortcuts for performing mathematical operations efficiently.
Q: Who invented Vedic maths?
Ans: Vedic Mathematics is not related to a single individual. It is a system of mathematical techniques that originated in ancient India and is based on Vedic literature.
Q: How many Vedic maths tricks are there?
Ans: Vedic Mathematics comprises a wide range of tricks and techniques that cover different mathematical operations. There isn’t a fixed number, as the system encompasses numerous methods for simplifying calculations.
Q: What are the three rules of Vedic maths?
Ans: The Vedic Mathematics is built on 16 Sutras (aphorisms) and 13 Sub-Sutras. While these sutras provide guiding principles for various calculations, there isn’t a specific set of “three rules” universally recognized in Vedic Maths.
Q: What are the 4 levels of Vedic Maths?
Ans: Vedic Mathematics doesn’t have different “levels” as different curriculum might have. Instead, vedic maths has a variety of techniques which can be applied to mathematical problems. These techniques range from basic arithmetic to more advanced calculations.












