Introduction of symmetry
Every real or imaginary object has a shape, symmetry can be defined as its edges, vertices, and angles between the two adjacent edges. Symmetry is the ability to divide these objects (including letters like “A”, “B”, etc.) into two or more identical parts, such that both parts look alike and appear as a mirror image of each other.
In this composition we will be looking about symmetrical shapes and pictures with names, if you want to know about a to z symmetry then continue with this blog.
Types of Symmetry And Its Relevance in Maths
There are various objects which can be found and the shape of these objects are distinct from each other. All these shapes have different ways of defining symmetry to them. Following are the types of symmetry which divide the figures in distinct manner according to suitable criteria.
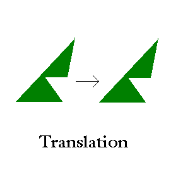
Translational Symmetry
Translational symmetry, also known as slide symmetry, occurs when a figure is shifted along a certain direction or angle while maintaining its shape then it can be referred as translational symmetry. Examples: Triangle, Circle.
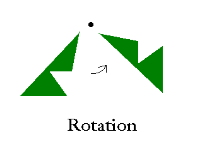
Rotational Symmetry
Rotational symmetry is observed when a figure can be rotated around a point, often the center, by a certain angle and still appears the same.
A classic example of rotational symmetry is a circle, as it looks unchanged after any rotation around its center. Examples: Square when rotated to 90 degrees remain unchanged.
Reflexive Symmetry
Reflexive symmetry is a type of symmetry in which one half of the object appears to be the same as the other half.
Examples of Reflexive symmetry can be often seen in dragonflies and butterflies (when divided in half that seems to be identical).
Examples: The letter “A” is also an example of reflexive symmetry shape.

Glide Symmetry
Glide symmetry, a combination of translational and reflectional symmetry, involves sliding a figure along a line while also reflecting it.
Examples: Motion of a skater gliding and reflecting off an ice surface or a leaf which is being dragged on the ground.

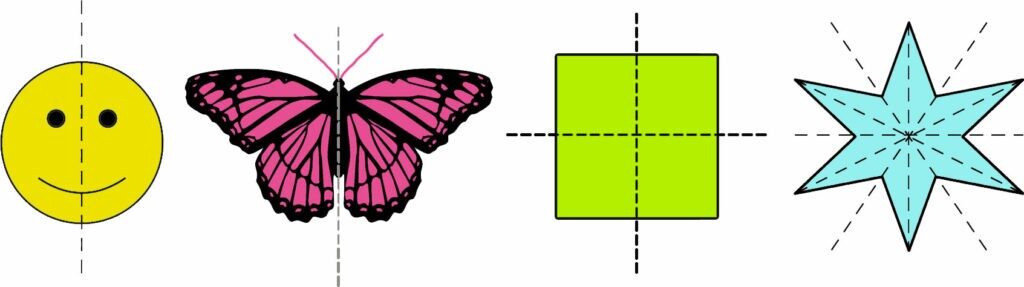
Line of Symmetry
A line of symmetry is a line that divides a figure into two mirrored halves, where each half appears to be the reflection of each other. There are different ways through which these lines can cut a figure in two identical parts, for each figure these lines can be of different types in context of the way it divides a figure. Hence, there are different types of lines of symmetry which are discussed below:
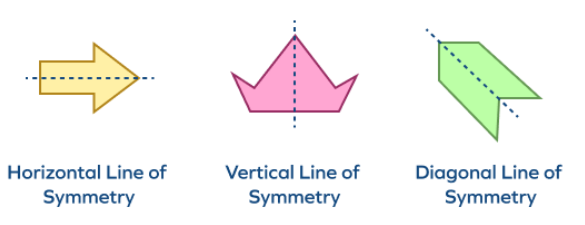
Vertical Line of Symmetry
A vertical line of symmetry is a line which runs vertically and divides a figure into two mirror images or identical parts. The letter “M” is a good example, as it can be split into two identical parts when divided vertically.
Horizontal Line of Symmetry
A horizontal line of symmetry is a line which runs horizontally through a figure, creating two symmetrical halves. A figure which is identical at top and bottom is referred to as horizontally symmetrical. Like the numeral “8” shows horizontal symmetry, as its upper and lower parts are reflections of each other.
Diagonal Line of Symmetry
The line which connects opposite edges together is called a diagonal, And when this line cuts through figures at an angle, creating two symmetrical halves, then this line is known as Diagonal line of symmetry. This line of symmetry is mainly used in shapes like square, rhombus, etc which can be divided into two identical parts through diagonal.
Symmetry in Real Life
There are different structures which can be found around in nature and some which are human made which prevails to be symmetric.
Examples: The wings of butterflies and dragonflies, the arrangement of flower petals, and even architectural symmetry projects are made by the use of the concept of symmetry to give a more aesthetic and appealing look.

Conclusion – Symmetry in Math
Symmetry is a property that involves dividing a figure(shapes) into two or more identical parts, where one part appears to be the mirror image of the others. Symmetry is the mathematical concept which is used to divide an object(figure) into identical parts on different planes of symmetry. That’s all about the conclusion of symmetry.
Download PPT of Symmetry in Math

Video On Symmetry in Math
FAQs – Symmetry in Math
Q. What does symmetry mean in math?
Ans. Symmetry is defined as the ability to divide these objects into two or more identical parts, such that both the parts look alike and appear as a mirror image of each other.
Q. What are the 4 types of symmetry?
Ans. The four types of symmetry are translational symmetry, rotational symmetry, reflexive symmetry, and glide symmetry.
Q. What is an example of radial symmetry?
Ans. A starfish is an example of radial symmetry, where its body parts radiate from a central point.
Q. What is linear symmetry?
Ans. Linear symmetry, also known as reflectional symmetry, occurs when a figure can be divided into two mirror image halves (Two Identical Halves).
Q. What is an example of horizontal symmetry?
Ans. The capital letter “B” demonstrates horizontal symmetry, as its upper and lower parts mirror each other.












